MATLAB-FOQUS interface - tutorials

Problem Statement: Steady-State Continuous Stirred Tank Reactor (CSTR)

This example solves a non-linear system of equations which describes a mathematical model for a Continuous Stirred Tank Reactor (CSTR) at steady state. The CSTR is cooled with a cooling coil, and a simple exothermic reaction takes place inside the reactor (see Figure 1). Model main assumptions: 1) the reactant is perfectly mixed, and 2) the volume, heat capacities and densities are constants. Further details regarding the model are given in Vojtesek and Dostal, 2011.

Source: Jiri Vojtesek and Petr Dostal. Use of MATLAB Environment for Simulation and Control of CSTR. International Journal of Mathematics and Computers in Simulation, 6(5), 2011.

Figure 1 - Representation of a CSTR with exothermic reaction

The CSTR model in steady-state is represented by the following non-linear system of equations, which was obtained from mass and energy balances of the reactant and cooling.

\[\mathrm{a_{1}\cdot\left(T_{0}-T\right)+a_{2}\cdot k_{1}\cdot c_{A}+a_{3}\cdot q_{c}\cdot\left(1-e^{\frac{a_{4}}{q_{c}}}\right)\cdot\left(T_{c0}-T\right)=0}\]

\[\mathrm{a_{1}\cdot\left(c_{A0}-c_{A}\right)-k_{1}\cdot c_{A}=0}\]

\[\mathrm{k_{1}=k_{0}\cdot e^{\frac{-E}{R\cdot T}}}\]

\[\mathrm{q_{0}=q}\]

\[\mathrm{q_{c0}=q_{c}}\]

where \(\mathrm{a_{1-4}}\) are constants calculated as follows:

\[\mathrm{a_{1}=\frac{q}{V};\quad a_{2}=\frac{-\Delta H}{\rho\cdot c_{p}};\quad a_{3}=\frac{\rho_{c}\cdot c_{pc}}{\rho\cdot c_{p}\cdot V};\quad a_{4}=\frac{-h_{a}}{\rho_{c}\cdot c_{pc}}}\]

The fixed parameters of the system are given below.

Parameter	Symbol [Unit]	Value
Reactor’s volume	\(\mathrm{V\:[l]}\)	100
Reaction rate constant	\(\mathrm{k_{0}\:[min^{-1}]}\)	7.2e10
Activation energy divided by R	\(\mathrm{E/R\:[K]}\)	1e4
Reactant’s feed temperature	\(\mathrm{T_{0}\:[K]}\)	350
Inlet coolant temperature	\(\mathrm{T_{c0}\:[K]}\)	350
Reaction heat	\(\mathrm{\Delta H\:[cal\cdot mol^{-1}]}\)	-2e5
Specific heat of the reactant	\(\mathrm{c_{p}\:[cal\cdot g^{-1}\cdot K^{-1}]}\)	1
Specific heat of the cooling	\(\mathrm{c_{pc}\:[cal\cdot g^{-1}\cdot K^{-1}]}\)	1
Density of the reactant	\(\mathrm{\rho\:[g\cdot l^{-1}]}\)	1e3
Density of the cooling	\(\mathrm{\rho_{c}\:[g\cdot l^{-1}]}\)	1e3
Feed concentration	\(\mathrm{c_{A0}\:[mol\cdot l^{-1}]}\)	1
Heat transfer coefficient	\(\mathrm{h_{a}\:[cal\cdot min^{-1}\cdot K^{-1}]}\)	7e5
Volumetric flow rate of reactant	\(\mathrm{q_{0}\:[l\cdot min^{-1}]}\)	100
Volumetric flow rate of cooling	\(\mathrm{q_{c0}\:[l\cdot min^{-1}]}\)	80

The variables in the system of equations are described below:

Variable	Symbol [Unit]
Final reactant concentration	\(\mathrm{c_{A}\:[mol\cdot l^{-1}]}\)
Volumetric flow rate of products	\(\mathrm{q\:[l\cdot min^{-1}]}\)
Volumetric flow rate of cooling	\(\mathrm{q_{c}\:[l\cdot min^{-1}]}\)
Product temperature	\(\mathrm{T\:[K]}\)
Reaction rate	\(\mathrm{k_{1}\:[min^{-1}]}\)
Conversion	\(\mathrm{X_{A}\:[-]}\)

The conversion of reactant A is defined as:

\[\mathrm{X_{A}=\frac{c_{A0}-c_{A}}{c_{A0}}}\]

Tutorial 1: MATLAB - FOQUS direct

Step 1: Flowsheet Setup - create a node simulation in the FOQUS flowsheet editor, and name it “CSTR_Steady_State”.

Figure 2 - Flowsheet Setup

Step 2: Define all input and output variables of the model as described in Figures 3 and 4.

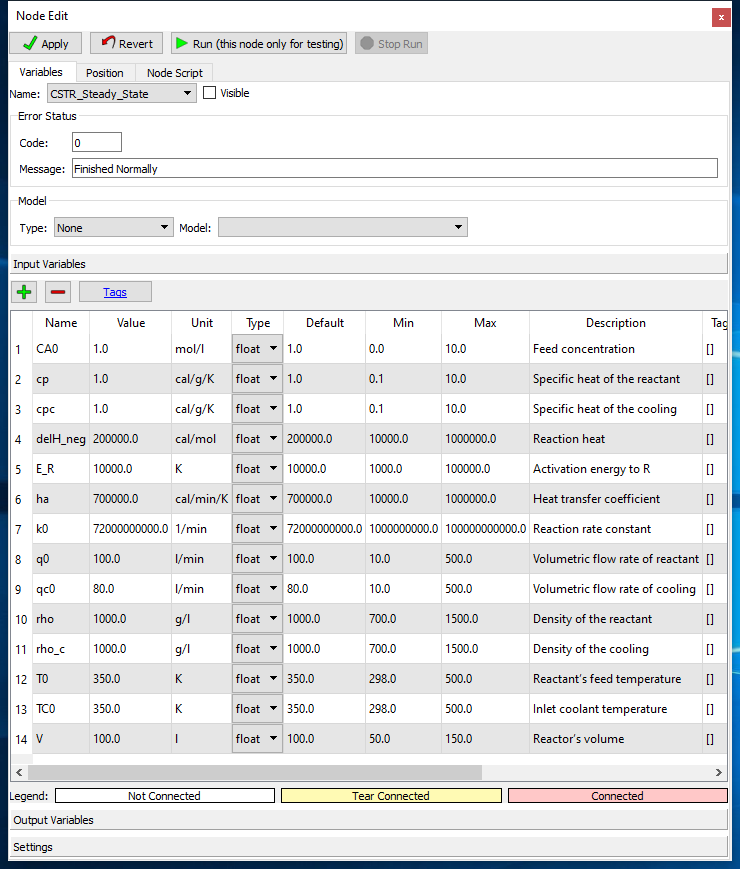
Figure 3 - Input Variables

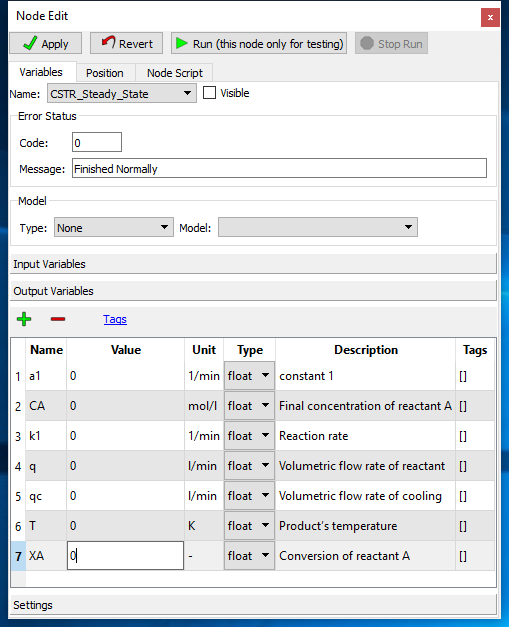
Figure 4 - Output Variables

Step 3: Create a MATLAB function solving the non-linear system of equations presented above. The MATLAB function file (along with the FOQUS file for this example) can be found in the folder: examples/tutorial_files/MATLAB-FOQUS/Tutorial_1

Note

The examples/ directory refers to the location where the FOQUS examples were installed, as described in Install FOQUS Examples.

Step 4: Load FOQUS plugin named “matlab_fs” in the simulation node as shown Figure 5. In the node editor, under “Type” option, choose “plugin”, and under “Model” option choose “matlab_fs”.

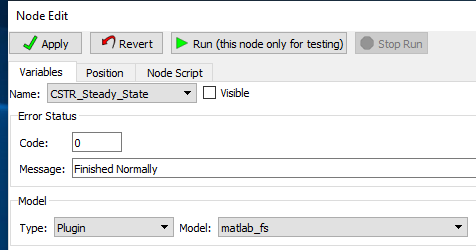
Figure 5 - FOQUS plugin for MATLAB-FOQUS interface

Step 5: In the Node Script tab write the code as shown in Figure 6.

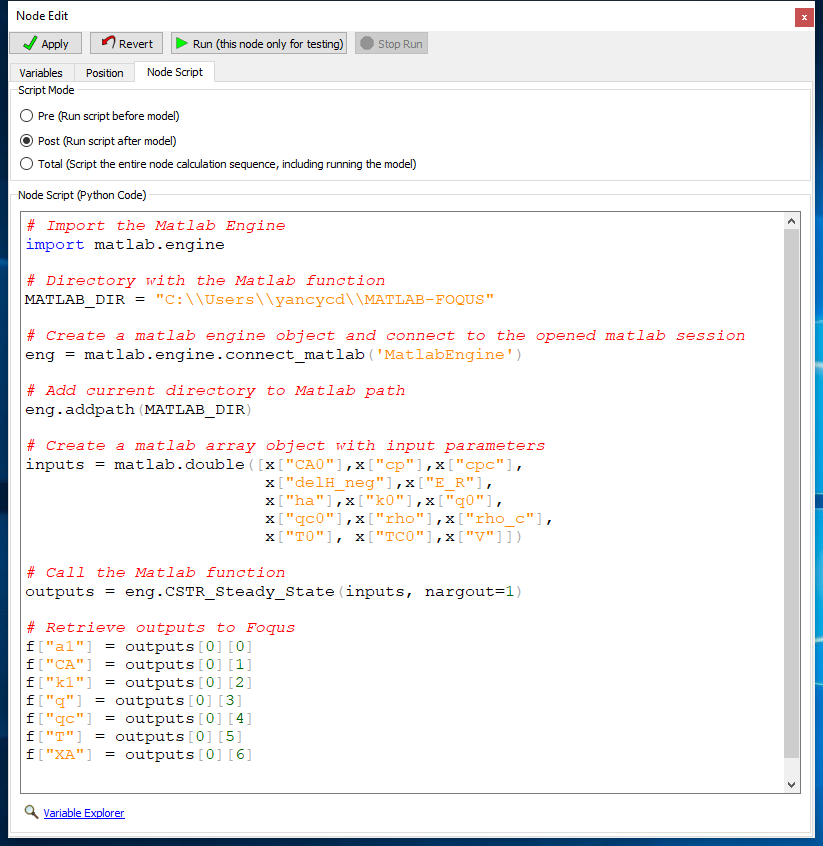
Figure 6 - Node Script Code

Note

The code shown in Figure 6 is intended to: 1) connect to the current MATLAB session, 2) create a MATLAB array object containing the input parameters for the MATLAB model, 3) Call the MATLAB function/model, and 4) Retrieve the outputs from the MATLAB function to FOQUS output variables.

• The code is below:

  # Import the Matlab Engine
  import matlab.engine
  
  # Directory with the Matlab function
  MATLAB_DIR = "C:\\Users\\yancycd\\MATLAB-FOQUS"
  
  # Create a matlab engine object and connect to the opened matlab session
  eng = matlab.engine.connect_matlab('MatlabEngine')
  
  # Add current directory to Matlab path
  eng.addpath(MATLAB_DIR)
  
  # Create a matlab array object with input parameters
  inputs = matlab.double([x["CA0"],x["cp"],x["cpc"],
           x["delH_neg"],x["E_R"],
           x["ha"],x["k0"],x["q0"],
           x["qc0"],x["rho"],x["rho_c"],
           x["T0"], x["TC0"],x["V"]])
  
  # Call the Matlab function
  outputs = eng.CSTR_Steady_State(inputs, nargout=1)
  
  # Retrieve outputs to Foqus
  f["a1"] = outputs[0][0]
  f["CA"] = outputs[0][1]
  f["k1"] = outputs[0][2]
  f["q"] = outputs[0][3]
  f["qc"] = outputs[0][4]
  f["T"] = outputs[0][5]
  f["XA"] = outputs[0][6]
  

Step 6: Run the node simulation to test if the simulation is working properly.

Step 7: Under the uncertainty tab in FOQUS, select Add New option to generate a new simulation ensemble. Select Use Flowsheet option. Fix all variables except the volume, which will be a variable with bounds 50-150 l. Select Latin Hypercube sampling method with 100 samples, and then generate the samples. Figure 7 represents the simulation ensemble generation.

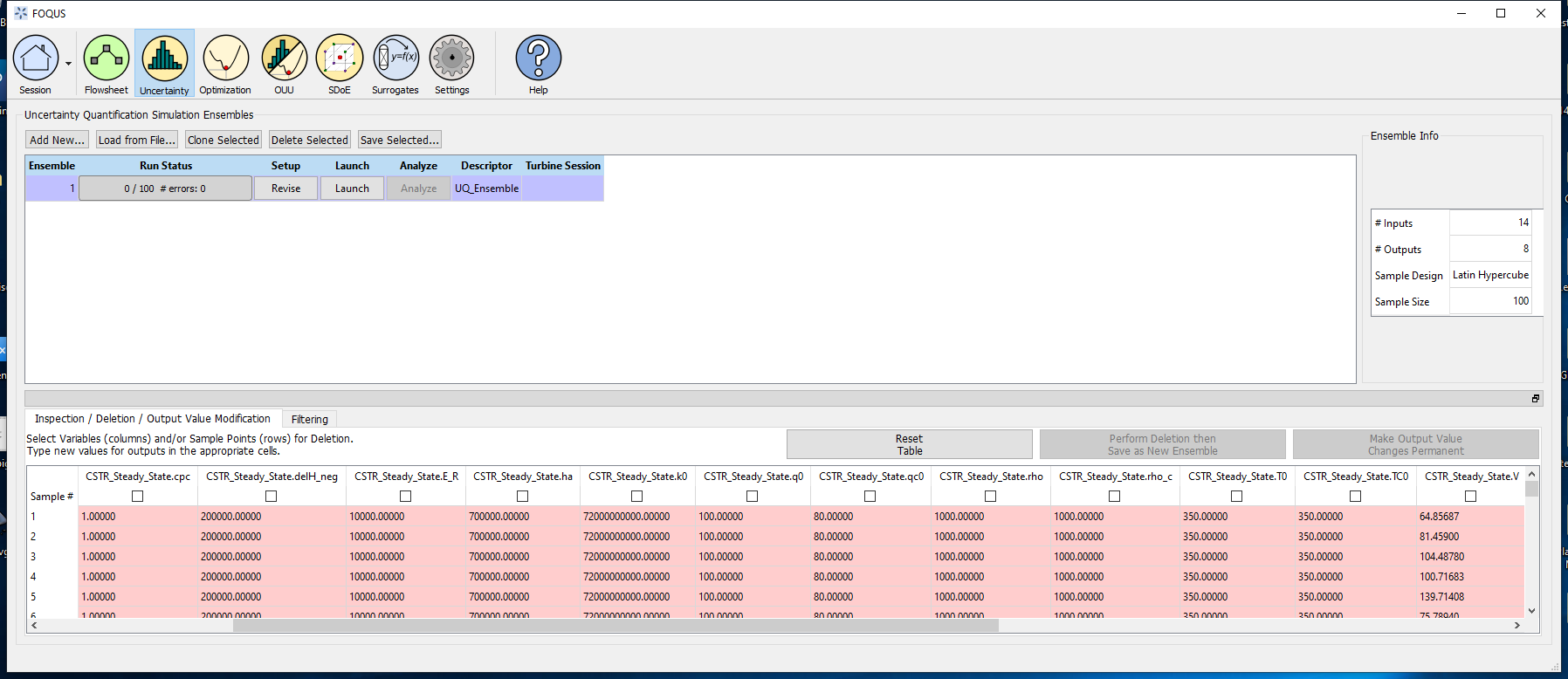
Figure 7 - Ensemble Generation

Step 8: Launch the simulations. Figure 8 represents the simulation results.

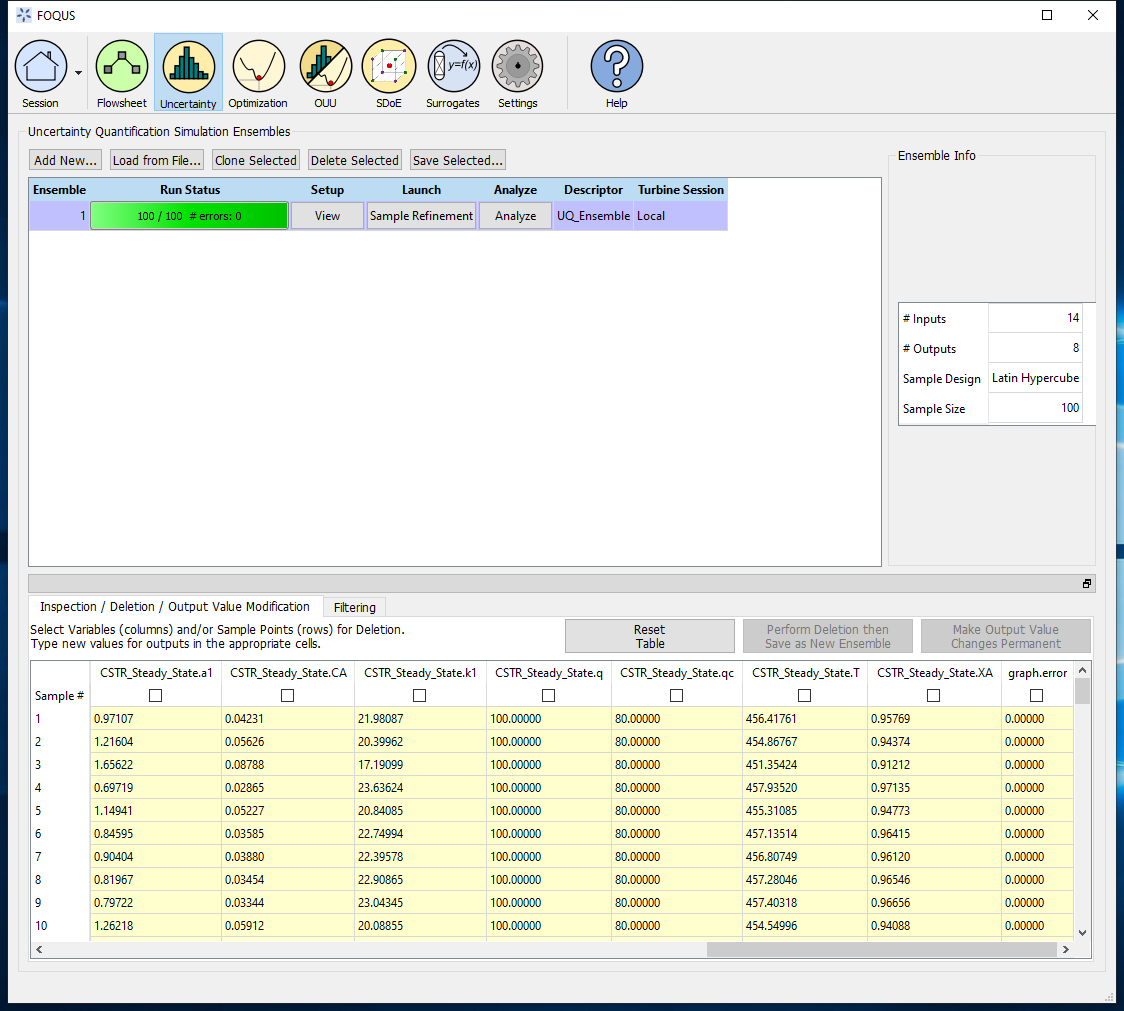
Figure 8 - Ensemble Results

Now, plotting the conversion vs the reactor’s volume, a similar figure to Figure 9 must be obtained.

Figure 9 - Conversion of Reactant A vs Reactor’s Volume

Tutorial 2: MATLAB script implementation

Step 1: Follow steps 1-3 from the Tutorial 1: MATLAB - FOQUS direct section. Users need to take care when defining the MATLAB function for the model in step 3 as it is necessary to define the MATLAB function inputs in the same order as were defined in the FOQUS flowsheet.

Step 2: Follow step 6 from the Tutorial 1: MATLAB - FOQUS direct section to generate a new simulation ensemble.

Step 3: Select the new generated UQ_Ensemble and click on Save Selected to save the ensemble as a PSUADE file. Choose a folder to save the file and name it as data.dat.

Step 4: Create a new MATLAB script to call the matlab_foqus_script.m file (which is distributed with FOQUS and can be found in examples/tutorial_files/MATLAB-FOQUS/Tutorial_2), and pass to it the MATLAB function containing the model. Below is an example of the code that needs to be executed. In examples/tutorial_files/MATLAB-FOQUS/Tutorial_2 you can find a MATLAB file name example_2_matlab_foqus.m with the code, and you can simply execute it:

% This is the path where the MATLAB model, the "matlab_foqus_script.m" file and the PSUADE file "data.dat" are located
path = "C:\Users\yancycd\MATLAB-FOQUS\";
% This is the PSUADE file name
PsuadFileName = 'data.dat';
% This is the MATLAB function name that contains the model
MatlabFunctionName = @(x) CSTR_Steady_State(x);
% Call the "matlab_foqus_script.m" file
matlab_foqus_script(MatlabFunctionName, PsuadFileName, path)

Note

After executing the code above, a new outputs.csv is created with the sample results from MATLAB. This is a file fully compatible with FOQUS.

Step 5: Under the uncertainty module, click on Load from File. Then choose .csv format file option and select the outputs.csv file created in the previous step. A new window will ask you the number of inputs that contain the outputs.csv file (see Figure 10), for this example is 14.

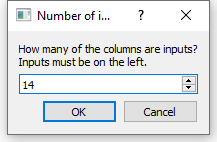
Figure 10 - Number of Inputs in the Outputs File

Step 6: Now, you have a new ensemble named “output.csv” with all input and outputs variables (see Figure 11), which can be used for other advanced analysis in the uncertainty module or any other FOQUS module.

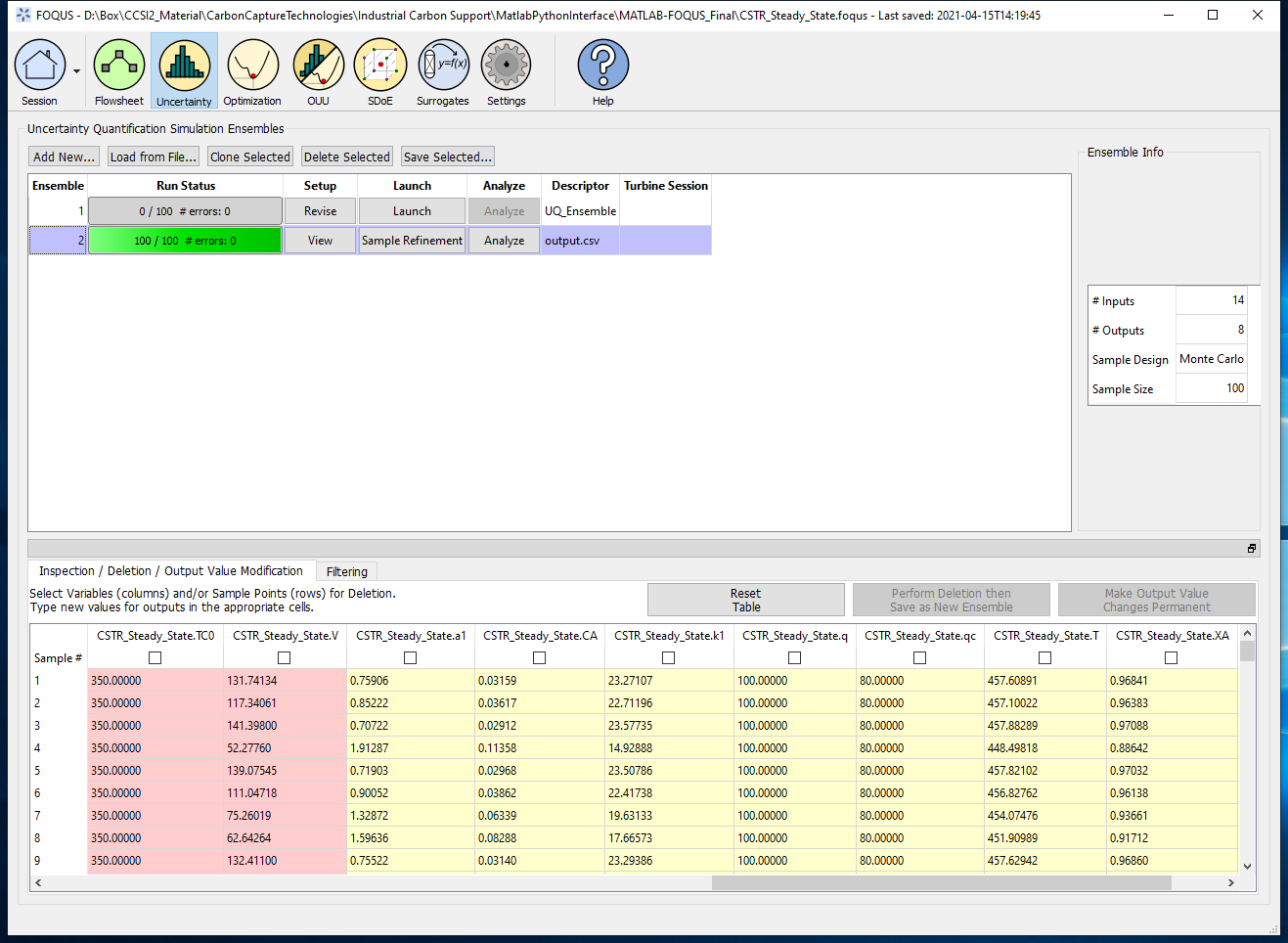
Figure 11 - New Ensemble with MATLAB Results

If you plot the conversion vs the reactor’s volume, you should get the Figure 9.